학교수학체험부스
-
- 행사명
- 2024 경남체험수학축전 ‘수학, 세상을 품다!’
-
- 일시
- 2024. 10. 26.(토) 10:00~16:00
-
- 장소
- 양산 워터파크
-
- 대상
- 초·중·고등학생, 학부모, 교직원
-
- 참여방법
- 현장예약
1대칭을 이용한 나만의 피젯스피너&팽이 만들기
-
- 부스번호
- 1
-
- 학교명/지도교사
- 미천초등학교 / 정기환
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 선대칭은 어떤 도형의 직선을 중심으로 대칭시켰을 때 겹치는 모양이다. 즉, 어떤 도형이 한 직선을 중심으로 선대칭인 것은 이 직선을 접는 선으로 하여 접었을 때 완전히 겹친다는 것을 뜻한다. 선대칭도형은 대응변의 길이와 대응각의 크기는 각각 같으며, 대응점을 이은 선분은 대칭축에 의하여 이등분되고 대칭축과 수직으로 만나는 특징이 있다.
상위메뉴로 이동
2전통등에서 찾은 곱셈
-
- 부스번호
- 2
-
- 학교명/지도교사
- 월촌초등학교/ 김진숙, 김병국
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 곱해지는 수와 곱하는 수의 일의 자리 수를 곱한 값과, 곱해지는 수와 곱하는 수의 십의 자리 수를 곱한 값을 더한다.
상위메뉴로 이동
3도형 마술퍼즐 세계로 체험하기 - 도형 분할 역설의 세계
-
- 부스번호
- 3
-
- 학교명/지도교사
- 진영대흥초등학교 / 정유경, 정용식
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 사라지는 퍼즐이란 어떤 이미지가 사라지거나 변하는 것을 설명하는 것이 목표인 퍼즐이다. 분명히 동일한 조각을 가지고서 배치만 달리한 것인데 신기하게도 면적이 바뀌거나 특정 이미지가 없어지는 현상이 발생한다. 우리가 관찰하기에는 처음에는 작게 나눈 조각들이 모여서 초기 도형과 같은 크기와 형태를 가지는 것처럼 보이지만, 실제로는 전체 면적이나 길이가 변화된다.
상위메뉴로 이동
4뒤틀린 입체도형 만들기
-
- 부스번호
- 4
-
- 학교명/지도교사
- 칠산초등학교 / 윤성경
-
- 점심시간
- 12:30~13:30
-
- 부스소개
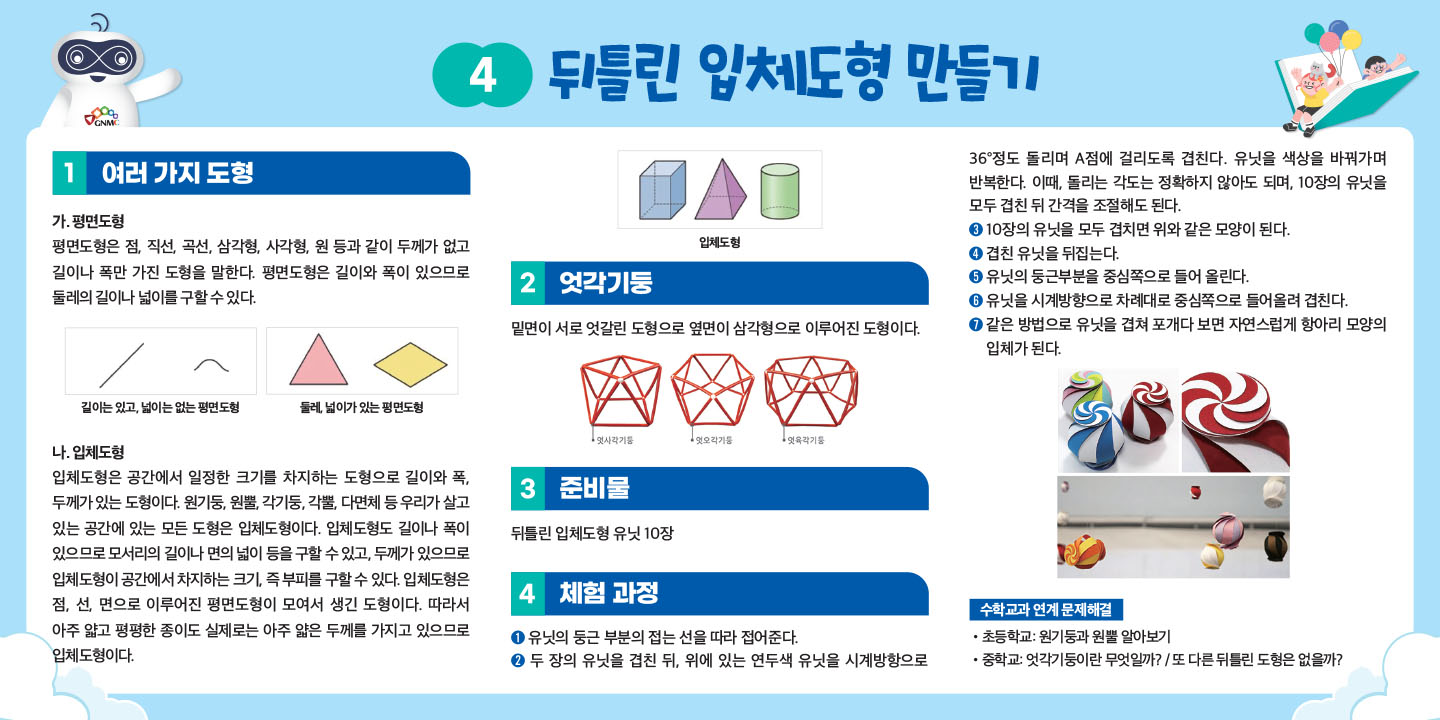
- 평면도형은 점, 직선, 곡선, 삼각형, 사각형, 원 등과 같이 두께가 없고 길이나 폭만 가진 도형을 말한다. 평면도형은 길이와 폭이 있으므로 둘레의 길이나 넓이를 구할 수 있다. 입체도형은 공간에서 일정한 크기를 차지하는 도형으로 길이와 폭, 두께가 있는 도형이다. 원기둥, 원뿔, 각기둥, 각뿔, 다면체 등 우리가 살고 있는 공간에 있는 모든 도형은 입체도형이다.
상위메뉴로 이동
5그래비트랙스로 만나는 수학
-
- 부스번호
- 5
-
- 학교명/지도교사
- 가양초등학교 / 김예송
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 그래비트랙스는 액션 스톤이 목표 지점에 도달할 수 있도록 다양한 부품을 이용하여 나만의 트랙을 건설하는 보드게임입니다. 액션 스톤이 도착점에 잘 도착하도록 트랙을 설계하여 만들고 시행착오를 겪으며 도전하는 과정은 수학과의 문제 해결 전략을 탐색하고, 계획을 실행하고 반성하는 과정과 같습니다.
상위메뉴로 이동
6정폭도형바퀴 자동차 만들기
-
- 부스번호
- 6
-
- 학교명/지도교사
- 북정초등학교 / 이천호
-
- 점심시간
- 12:30~13:30
-
- 부스소개
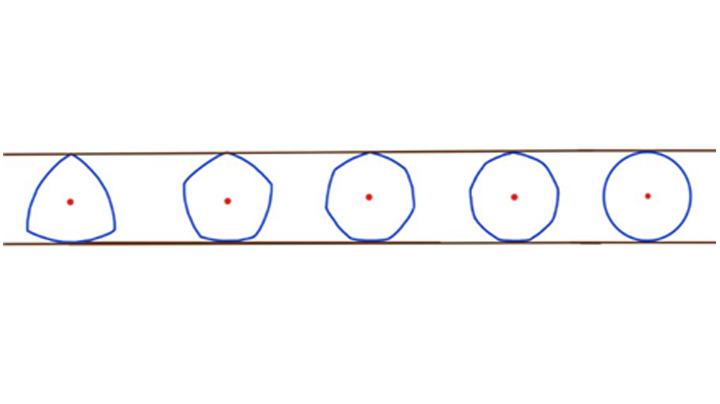
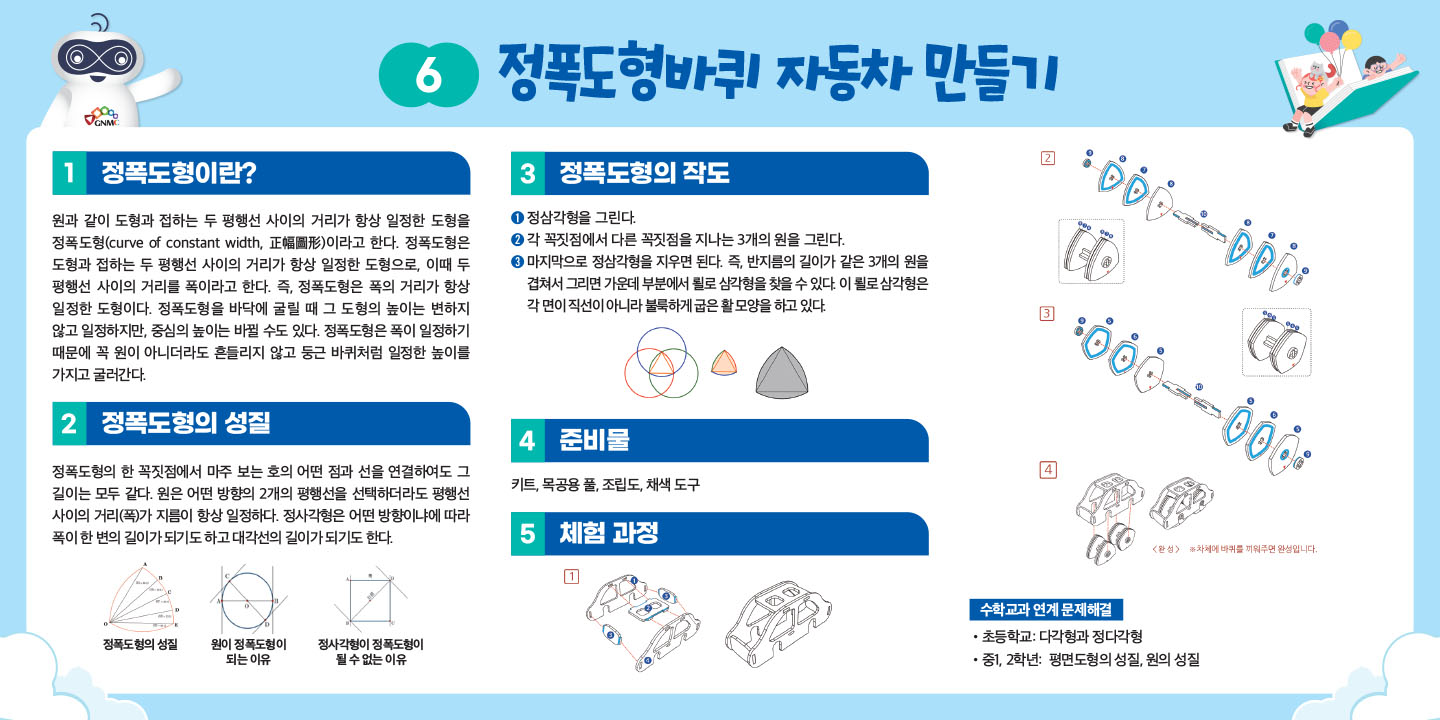
- 원과 같이 도형과 접하는 두 평행선 사이의 거리가 항상 일정한 도형을 정폭도형(curve of constant width, 正幅圖形)이라고 한다. 정폭도형은 도형과 접하는 두 평행선 사이의 거리가 항상 일정한 도형으로, 이때 두 평행선 사이의 거리를 폭이라고 한다. 즉, 정폭도형은 폭의 거리가 항상 일정한 도형이다.
상위메뉴로 이동
7달력으로 만드는 매직큐브
-
- 부스번호
- 7
-
- 학교명/지도교사
- 양산초등학교 / 신선영
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 매직큐브(Magic Cube)란 요시모토 나오키라는 디자이너가 1971년에 고안한 요시모토 큐브(Yoshimoto Cube)에서 비롯된 것으로, 8개의 큐브(정육면체)가 연결되어 끊임없이 풀어졌다가 접히는 순환 접음이 가능한 형태의 큐브를 말한다.
상위메뉴로 이동
8시에르핀스키 피라미드 만들기
-
- 부스번호
- 8
-
- 학교명/지도교사
- 영천초등학교 / 김승준, 양은아
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 프랙탈(fractal)이란 작은 구조가 전체 구조와 비슷한 형태로 끝없이 되는 구조를 의미한다. 이 용어는 프랑스 수학자 만델브로트(Benoit B. Mandelbrot) 박사가 1975년 ‘쪼개다’라는 뜻을 가진 라틴어 ‘프랙투스(frāctus)’에서 따와 처음 만들었다.
상위메뉴로 이동
9블렌디드로 메타버스 수학자 탐구
-
- 부스번호
- 9
-
- 학교명/지도교사
- 오봉초등학교 / 윤태영, 오성환, 이다은
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 메타버스는 “① 가상과 현실이 융합된 공간에서, ② 사람·사물이 상호작용하며, ③ 경제·사회·문화의 가치를 창출하는 가상 세계”를 뜻한다. 위 정의에서 우리가 알 수 있는 것은 단순 체험을 넘어 새로운 가치를 창출할 수 있는 가상 세계임을 알고 우리가 새로운 가치를 창출할 수 있도록 고민하는 것이다.
상위메뉴로 이동
10피라미드의 비밀을 풀어라! - VR 수학 방탈출 체험
-
- 부스번호
- 10
-
- 학교명/지도교사
- 영운초등학교 / 김수현, 박현진
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 코스페이시스(Cospaces)는 가상 현실(VR)과 증강 현실(AR)을 통해 학습 경험을 제공하는 플랫폼이다. 본 활동은 학생들이 코스페이시스를 통해 입체 가상현실 속 수학 방탈출 게임을 제작하고, 참가자들은 VR을 활용해 여러 문제를 풀며 보물상자의 비밀번호를 찾아내는 경험을 하게 된다. 특히, 입체도형을 직접 조작해보며 수학적 개념을 체험할 수 있다는 점이 핵심이다.
상위메뉴로 이동
11세계 수학자를 품은 슈링클스 나만의 열쇠고리 만들기
-
- 부스번호
- 11
-
- 학교명/지도교사
- 용산초등학교 / 박재수
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 슈링클스(Shrinkles)는 영국의 Key Craft Ltd 사에서 생산하는 특수한 종이 형태의 공예 소재이다. 이 종이는 열을 가하면 크기가 1/7로 작아지고 두께는 7배로 늘어나면서 딱딱한 플라스틱으로 바뀐다. 이렇게 열을 가했을 때 종이의 크기가 변형되는 이유는 슈링클스가 열가소성 플라스틱인 ‘폴리스티렌’으로 만들어졌기 때문이다.
상위메뉴로 이동
12정폭도형 레진아트 키링 만들기
-
- 부스번호
- 12
-
- 학교명/지도교사
- 옥포성지중학교/ 송현희, 김보형
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 정폭도형(正幅圖形)은 도형과 접하는 두 평행선 사이의 거리가 항상 일정한 도형으로, 이때 두 평행선 사이의 거리를 폭이라고 한다. 즉, 정폭도형은 폭의 거리가 항상 일정한 도형이다. 실생활 속에서도 정폭도형을 찾을 수 있는데, 실생활 정폭도형의 예시로는 콜로세움, 맨홀 뚜껑, 영국 동전, 로터리 엔진, 기타피크, 뢸로 삼각형 연필 등이 있다.
상위메뉴로 이동
13주사위의 변신은 무죄
-
- 부스번호
- 13
-
- 학교명/지도교사
- 밀양여자중학교 / 김현희
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 주사위는 놀이 도구의 하나로서, 일정 숫자에서 무작위로 선택된 어떤 결과를 얻고자 할 때 사용되는 장난감이다. 정다면체의 각각의 면에 임의의 숫자나 눈 등의 결괏값으로 얻고 싶은 후보가 되는 것들을 표시한 뒤 공중에 던져, 바닥에 떨어졌을 때 보이는 것(주로 윗면만)이 결과가 된다. 정육면체 모양의 주사위 한 개를 던졌을 때 나오는 경우의 수는 6가지며 특정 면이 나올 확률은 1/6이다.
상위메뉴로 이동
14음악 속의 수학세상(오르골)
-
- 부스번호
- 14
-
- 학교명/지도교사
- 미리벌중학교 / 한광미
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 피타고라스 학파는 “테트락티스”는 물체 무게를 수치로 나타낼 수 있듯이 사람의 귀에 전해지는 소리도 수치화할 수 있을 것이라고 생각했다. 피타고라스는 우연히 대장간 앞을 지나가다가 대장장이 4명이 서로 다른 망치로 쇠를 내리치는 소리를 듣고 사람의 귀를 즐겁게 하는 화음을 발견하게 된다. 또한, 소리와 진동수 사이의 연관성을 찾아 음과 수의 관계를 발견한다.
상위메뉴로 이동
15피타고라스 열쇠고리 만들기
-
- 부스번호
- 15
-
- 학교명/지도교사
- 범어중학교 / 김은희
-
- 점심시간
- 11:30~12:30
-
- 부스소개
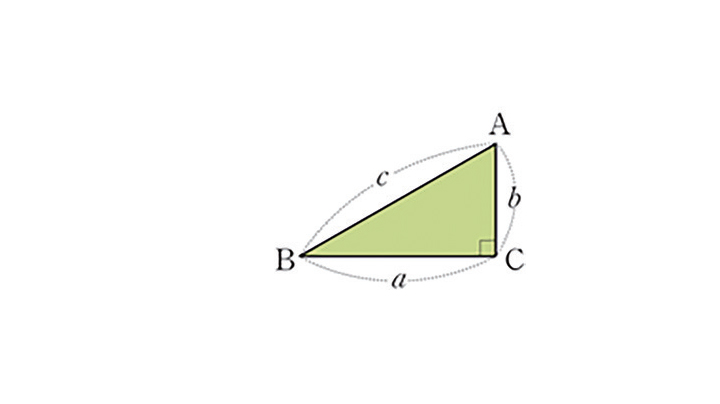
- 직각삼각형 ABC에서 직각을 낀 두 변의 길이를 각각 a,b라 하고, 빗변의 길이를 c라고 하면 a² + b² = c² 가 성립함을 알 수 있다. 즉, 직각삼각형에서 직각을 낀 두 변의 길이의 제곱의 합은 빗변의 길이의 제곱과 같음이 항상 성립하고, 이와 같은 직각삼각형의 성질을 피타고라스 정리라고 한다.
상위메뉴로 이동
16입체 스트링아트로 꽃병 만들기
-
- 부스번호
- 16
-
- 학교명/지도교사
- 물금동아중학교 / 신지연, 송재륜
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 일정한 규칙을 가지고 직선을 연속적으로 그려 아름다운 곡선을 만들거나 착시 현상을 일으키는 활동으로, 도형 안에 규칙적인 점을 찍은 다음 모든 점을 선으로 연결시켜 새로운 모양을 만들어내는 예술방식이다. 스트링아트는 평면상에서 점, 점과 점을 이은 선으로 구성되어 있으며 점을 규칙적으로 연결시킨 것이다. 각 점을 point, 선을 string 이라고 한다.
상위메뉴로 이동
17오더리 탱글(다면체) 만들기
-
- 부스번호
- 17
-
- 학교명/지도교사
- 양산여자중학교 / 고은경
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 겉보기에는 무질서해 보이지만 규칙적으로 꼬인 구조물을 ‘오더리 탱글(Orderly Tangle)’이라고 한다. ‘오더리’는 물건이 질서정연한 상태를 나타내는 단어고, ‘탱글’은 실이나 머리카락이 이리저리 엉킨 것을 뜻하는 단어다. 서로 뜻이 반대인 두 단어가 만난 오더리 탱글은 다각형이나 다면체가 규칙적으로 복잡하게 꼬여 서로 지탱하는 구조물이다.
상위메뉴로 이동
18하트 퍼즐 디자인하기
-
- 부스번호
- 18
-
- 학교명/지도교사
- 진주동명중학교 / 성필용
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 엮인 하트는 덴마크 등 북유럽에서 크리스마스트리 장식으로 사용한다. 엮인 하트의 정확한 기원은 알 수 없지만, 1860년 덴마크 작가 안데르센이 처음으로 시도했다는 설이 가장 유력하다. 그는 크리스마스트리를 장식하기 위해 하트 고리를 만들었다. 그러나 그가 제작한 하트는 고리가 없기 때문에, 실제로 장식용으로 사용되지는 않았다.
상위메뉴로 이동
19정다각형을 이용한 회전하는 팽이
-
- 부스번호
- 19
-
- 학교명/지도교사
- 진주동중학교 / 백경식
-
- 점심시간
- 11:30~12:30
-
- 부스소개
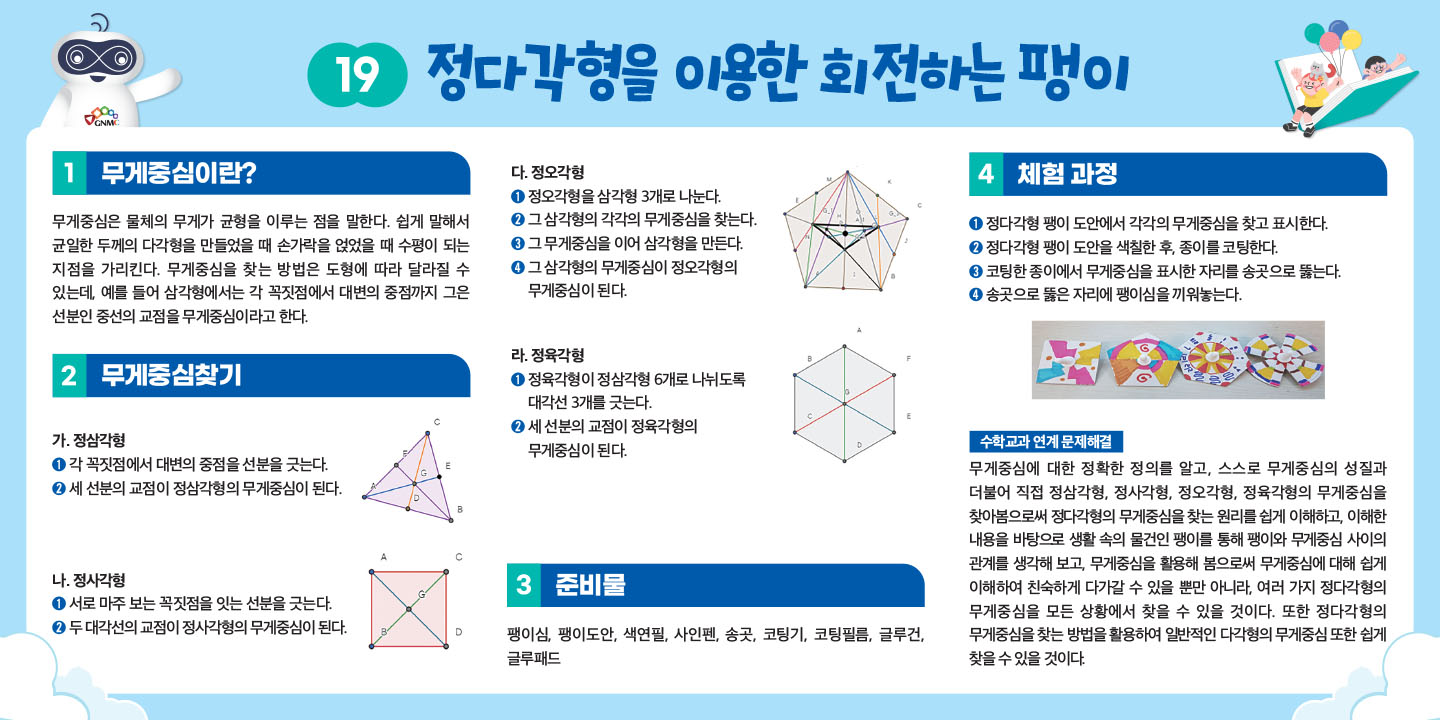
- 무게중심은 물체의 무게가 균형을 이루는 점을 말한다. 쉽게 말해서 균일한 두께의 다각형을 만들었을 때 손가락을 얹었을 때 수평이 되는 지점을 가리킨다. 무게중심을 찾는 방법은 도형에 따라 달라질 수 있는데, 예를 들어 삼각형에서는 각 꼭짓점에서 대변의 중점까지 그은 선분인 중선의 교점을 무게중심이라고 한다.
상위메뉴로 이동
20좌표평면과 레이저 각인
-
- 부스번호
- 20
-
- 학교명/지도교사
- 김해건설공업고등학교 / 이유지, 주진중
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 레이저 각인기는 미세하고 정밀한 작업을 필요로 하는 다양한 산업 분야에서 활용된다. 이 도구는 설정된 XY 좌표 평면을 따라 레이저 빔을 움직이며, 재료 표면에 텍스트, 로고, 그래픽, 또는 기타 디자인을 새기는 데 사용된다. 레이저 각인기는 일반적으로 목재, 금속, 유리, 플라스틱 등 다양한 재료에 적용할 수 있으며, 그 활용 범위는 매우 넓다. 레이저 각인기는 교육 현장에서도 활용될 수 있는데, 학생들이 직접 좌표를 설정하고 결과물을 확인함으로써 좌표 시스템에 대한 이해를 높일 수 있다.
상위메뉴로 이동
21펄러비즈로 보는 세상 - 나만의 패턴 만들기
-
- 부스번호
- 21
-
- 학교명/지도교사
- 김해삼문고등학교 / 손경수
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 우리가 현실 세계에서 흔히 볼 수 있는 사물, 동·식물, 자연을 들여다보면 점, 선, 면, 입체도형 등 도형의 기본 요소를 갖추고 있으며 분할, 반복, 대칭 등을 나타내는 규칙성이나 곡선과 같은 불규칙성이 아름답게 조화를 이루는 수학적 심미성이 담겨 있습니다. 아이들이 이러한 수학의 매력과 아름다움을 펄러비즈를 사용한 제작 활동으로 느낄 수 있습니다.
상위메뉴로 이동
22피보나치 수열 그림과 머그컵의 콜라보
-
- 부스번호
- 22
-
- 학교명/지도교사
- 밀양동명고등학교 / 한유정, 박희도
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 피보나치 수열이란 0, 1, 1, 2, 3, 5, 8, 13, 21, …인 형태로 나타나는 수열로, 이 수열의 규칙을 관찰해보면 세 번째 이후의 항은 직전 두 항의 합으로 나타난다. 이 수열은 피보나치(L.Fibonacci)가 1202년 『산술(算術)의 서(書)』에서 처음으로 제기했었다. 이렇게 단순한 수열이 중요해진 이유는 이 수열이 자연계의 일반법칙을 나타내는 것으로 보이기 때문이다.
상위메뉴로 이동
23텐세그리티 구조로 수학과 밀당하기
-
- 부스번호
- 23
-
- 학교명/지도교사
- 양산여자고등학교 / 공유정, 허성돈
-
- 점심시간
- 11:30~12:30
-
- 부스소개
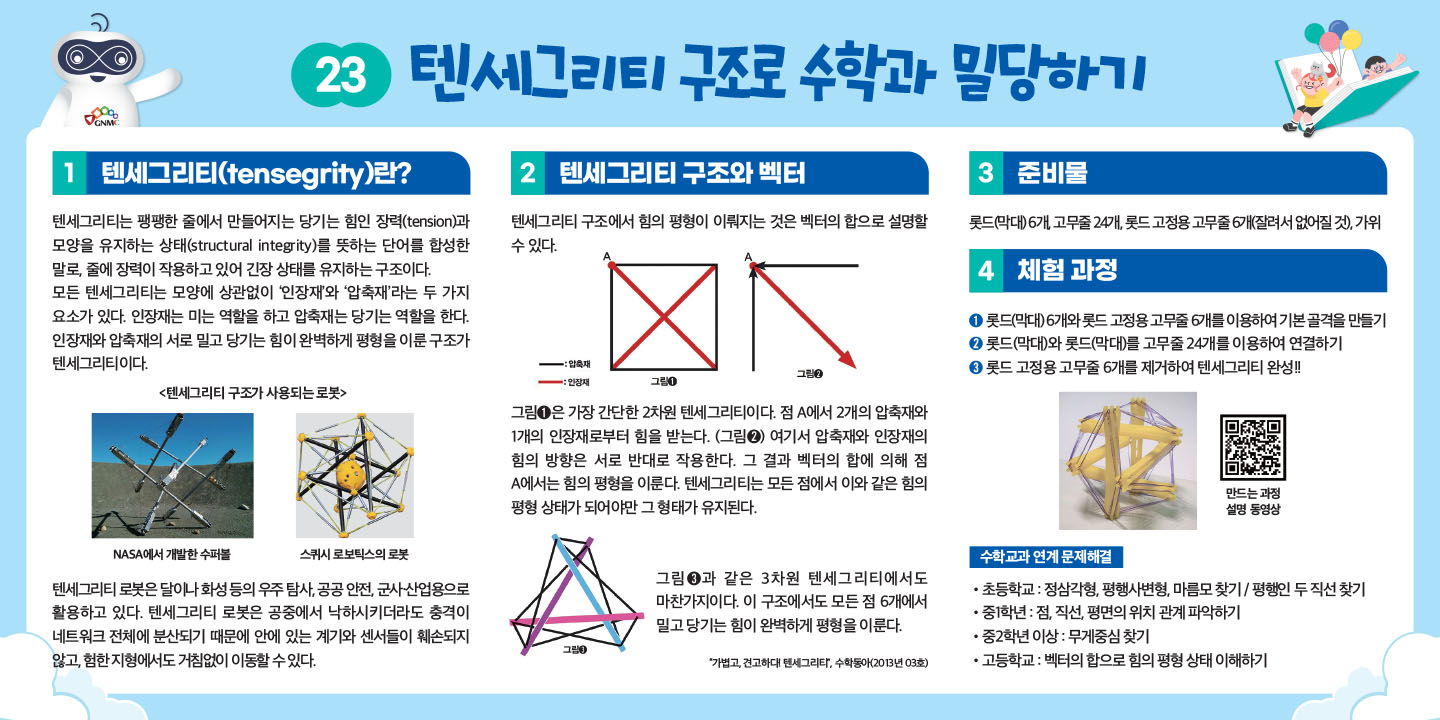
- 텐세그리티는 팽팽한 줄에서 만들어지는 당기는 힘인 장력(tension)과 모양을 유지하는 상태(structural integrity)를 뜻하는 단어를 합성한 말로, 줄에 장력이 작용하고 있어 긴장 상태를 유지하는 구조이다. 모든 텐세그리티는 모양에 상관없이 ‘인장재’와 ‘압축재’라는 두 가지 요소가 있다. 인장재는 미는 역할을 하고 압축재는 당기는 역할을 한다.
상위메뉴로 이동
24지금 잠에 들지 않으면, 스트링아트 무드등이 재워줄 거에요.
-
- 부스번호
- 24
-
- 학교명/지도교사
- 양산제일고등학교 / 신진석
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 스트링아트는 실, 핀, 못 등을 사용하여 다양한 패턴과 이미지를 만드는 예술 기법 이다. 이 기법은 기하학적 형태, 곡선, 심지어 구체적인 이미지까지도 표현할 수 있으며, 이를 통해 매우 독창적이고 아름다운 작품을 만들 수 있다. 스트링아트는 단순한 재료를 사용하지만, 복잡하고 정교한 결과물을 만들어낼 수 있다.
상위메뉴로 이동
25프렉탈 도형을 이용한 생명나무 워터볼 만들기
-
- 부스번호
- 25
-
- 학교명/지도교사
- 진해세화여자고등학교 / 김민정, 변성운
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 프랙탈(fractal)은 일부 작은 조각이 전체와 비슷한 기하학적 형태를 말한다. 이런 특징을 자기 유사성(Self-Similarity)이라고 하는데 자기 유사성을 갖는 구조는 전체적으로 보나 작은 일부분의 요소로 보나 비슷하거나 똑같아 보이는게 특징이다. 마치 자가증식을 해 커다란 하나의 객체를 만든 느낌을 주기도 한다. 그렇다면 왜 프랙탈이라고 할까?
상위메뉴로 이동
26태양광 자동차 만들기
-
- 부스번호
- 26
-
- 학교명/지도교사
- 진해세화여자고등학교 / 신용남, 최민주
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 태양의 빛 에너지를 전기에너지로 바꾸는 장치가 태양전지입니다. 태양전지는 전기적 성질이 다른 N(negative)형의 반도체와 P(positive)형의 반도체를 접합시킨 구조로 반도체의 pn접합에 빛을 비추면 광전효과*에 의해 광기전력*이 일어나는 것을 이용한 것입니다.
상위메뉴로 이동
27H 만들기, 12조각이용 구(공)만들기
-
- 부스번호
- 27
-
- 학교명/지도교사
- 증산고등학교 / 우형찬
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 창의적 사고란 발산적(확산적) 사고로서, 아이디어가 많고 다양하고, 독특한 것을 의미하며, 새롭고 유용한 아이디어를 생산해내는 정신적인 과정이고, 통상적인 것이 아니라 기발하거나 신기하며 독창적인 것이다. 또한, 유용하고 적절하며, 가치가 있어야 하고, 기존의 정보(지식, 상상, 개념 등)들을 특정한 요구조건에 맞거나 유용하도록 새롭게 조합시킨 것이다.
상위메뉴로 이동
28매듭이론을 적용한 파라코드팔찌만들기
-
- 부스번호
- 28
-
- 학교명/지도교사
- 진해중앙고등학교 / 황혜원
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 파라코드란 낙하산을 뜻하는 parachute의 para와 줄을 뜻하는 cord의 합성어로 낙하산 줄을 뜻하며 550 cord라고 부르기도 한다. 원래는 이름답게 제 2차 세계대전에서 미군이 낙하산과 몸을 연결하기 위해 사용한 나일론 줄 이었으나 다용도로 쓸모가 많고 가격도 싸서 등산인들이 널리 사용하며 알려지기 시작했다. 파라코드 한 가닥이 550 파운드(약 250kg) 무게를 버틸 수 있으므로 생존팔찌 또는 생명팔찌로 불리기도 한다.
상위메뉴로 이동
29트리스켈볼로 알아보는 대칭의 세계
-
- 부스번호
- 29
-
- 학교명/지도교사
- 진해중앙고등학교 / 최봉구
-
- 점심시간
- 11:30~12:30
-
- 부스소개
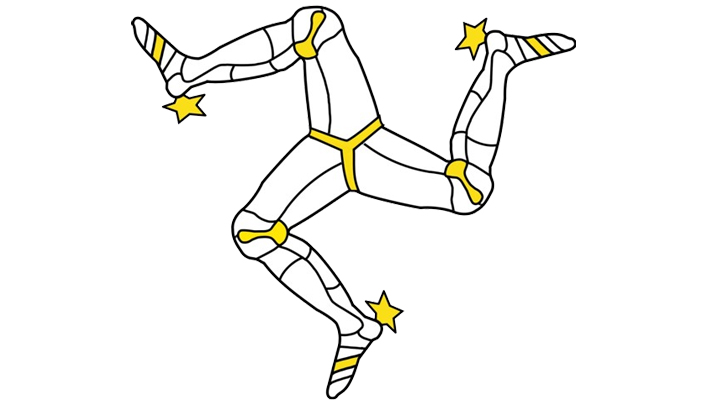
- 트리스켈리온(triskelion)은 세 개의 소용돌이나 사람의 다리 같은 곡선들이 중심에서 뻗어나가는 형태로 이루어진 디자인을 가진 문양이다. 고대 문명의 유물에서 발견되었으며 ‘3개의 다리’를 의미하는 그리스어 ‘tri’와 ‘skelos’에서 유래되었다. 3개의 나선형 대칭 소용돌이가 한 점에서 나타난 문양으로 가장 오래된 신비한 상징 중 하나이며 미케네, 그리스, 리키아, 팜필리아 등 고대 문명의 유물에서 발견되었다.
상위메뉴로 이동
30스트링아트 - 선의 아름다움
-
- 부스번호
- 30
-
- 학교명/지도교사
- 해성고등학교 / 김태욱, 서보인
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 스트링아트는 실을 이용하여 나무나 판 등의 표면에 모양이나 패턴을 만들어내는 예술적 기법이다. 주로 나무나 판 위에 못을 박고, 실을 감아가며 원하는 모양이나 패턴을 만들어낸다. 스트링아트는 기하학적 패턴이나 배의 돛과 같은 표현 디자인을 형성하기 위해 점 사이에 묶인 실을 배열하는 것이 특징이며, 예술 자료로 사용된다.
상위메뉴로 이동
31직사각형 퍼즐, 친환경 액자 만들기
-
- 부스번호
- 31
-
- 기관명
- 경남수학문화관 양산수학체험센터
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 로직 퍼즐 중의 하나로 사각 자르기 또는 사각형 나누기로 불리는 퍼즐이다. 2005년 일본 니코리사에서 시카구(Shikaku) 퍼즐로 발표되었고 도형감각, 공간감각을 키울 수 있는 퍼즐이다. 직사각형 퍼즐은 큰 직사각형 모양 게임판에 적힌 각각의 숫자대로 작은 직사각형으로 나누는 퍼즐이다. 직사각형 퍼즐 속 숫자는 그 숫자가 적힌 칸이 포함된 작은 직사각형을 이루는 칸의 개수다.
상위메뉴로 이동
32테셀레이션 텀블러백 만들기
-
- 부스번호
- 32
-
- 기관명
- 경남수학문화관 밀양수학체험센터
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 일정한 형태의 도형들로 평면을 빈틈없이 채우는 것. 평면작성, 타일링 등으로 불리기도 하며 ‘쪽매맞춤’ 혹은 ‘쪽매붙임’으로 번역되기도 한다. 같은 모양의 정다각형으로 테셀레이션을 하려면 정삼각형, 정사각형, 정육각형 밖에 불가능하지만 (이 세 개의 정다각형만이 한 각의 크기가 360의 약수이기 때문이다), 두 가지 이상의 정다각형을 활용해서 다양한 테셀레이션을 할 수 있다. 실생활에서는 목욕탕 타일이나 보도블록을 까는 것에서 쉽게 찾아볼 수 있을 것이다.
상위메뉴로 이동
33한붓그리기 네온사인 만들기
-
- 부스번호
- 33
-
- 기관명
- 경남수학문화관 진주수학체험센터
-
- 점심시간
- 11:30~12:30
-
- 부스소개
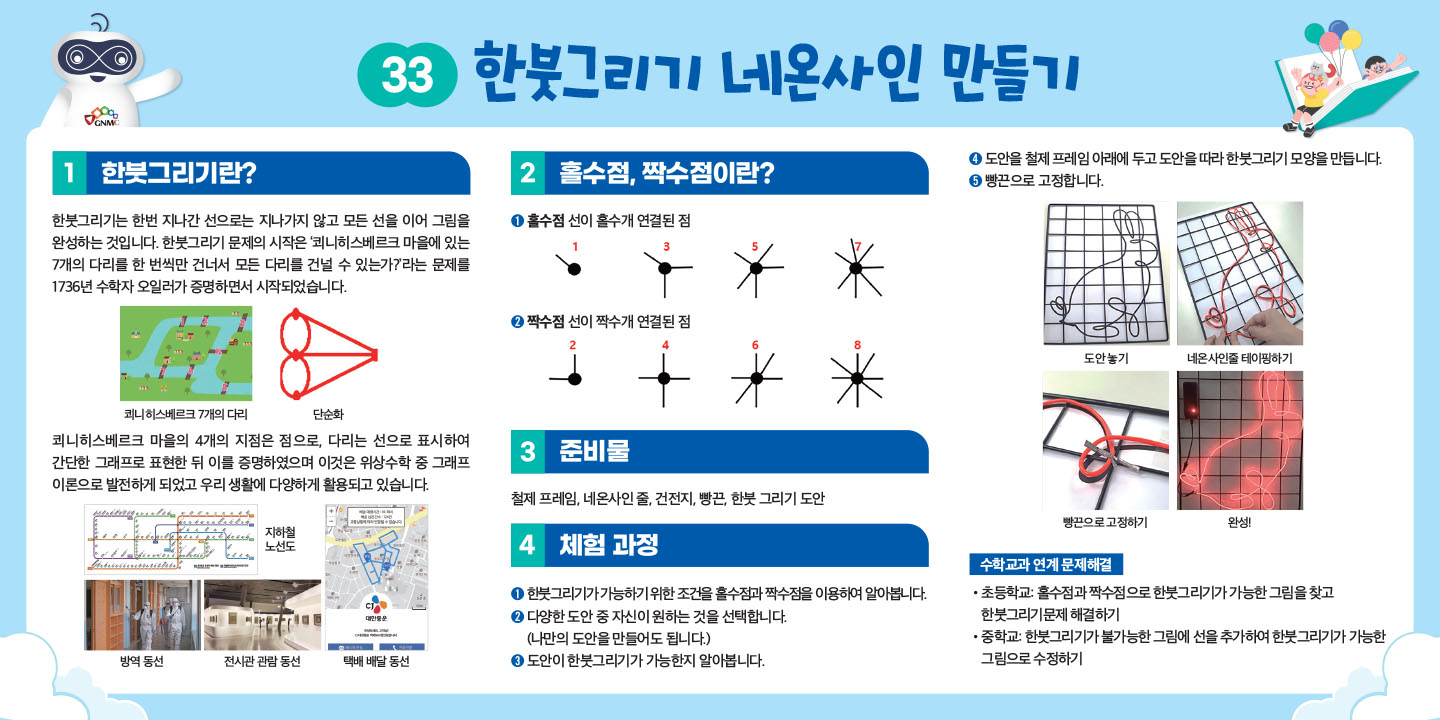
- 한붓그리기는 한번 지나간 선으로는 지나가지 않고 모든 선을 이어 그림을 완성하는 것입니다. 한붓그리기 문제의 시작은 ‘쾨니히스베르크 마을에 있는 7개의 다리를 한 번씩만 건너서 모든 다리를 건널 수 있는가?’라는 문제를 1736년 수학자 오일러가 증명하면서 시작되었습니다.
상위메뉴로 이동
34사각형으로 알아보는 샘로이드 퍼즐
-
- 부스번호
- 34
-
- 기관명
- 경남수학문화관 김해수학체험센터
-
- 점심시간
- 12:30~13:30
-
- 부스소개
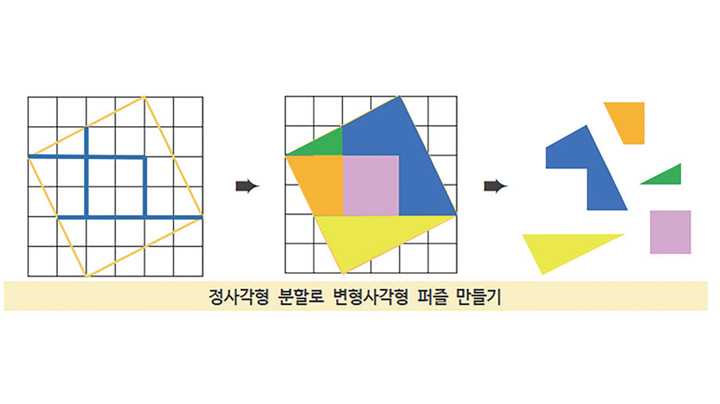
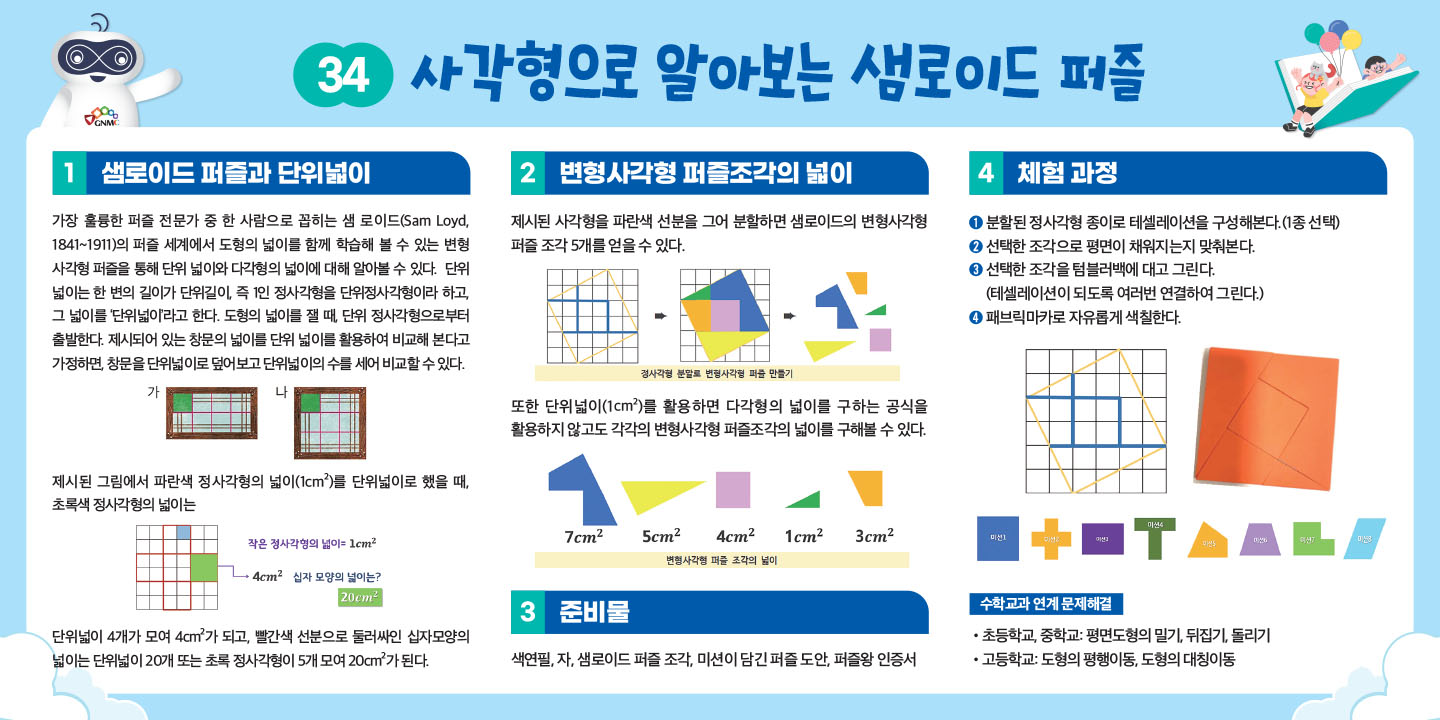
- 가장 훌륭한 퍼즐 전문가 중 한 사람으로 꼽히는 샘 로이드(Sam Loyd, 1841~1911)의 퍼즐 세계에서 도형의 넓이를 함께 학습해 볼 수 있는 변형 사각형 퍼즐을 통해 단위 넓이와 다각형의 넓이에 대해 알아볼 수 있다. 단위 넓이는 한 변의 길이가 단위길이, 즉 1인 정사각형을 단위정사각형이라 하고, 그 넓이를 ‘단위넓이’라고 한다. 도형의 넓이를 잴 때, 단위 정사각형으로부터 출발한다.
상위메뉴로 이동
35신기한 마술상자 만들기
-
- 부스번호
- 35
-
- 기관명
- 경남수학문화관 거창수학체험센터
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 인류의 문명이 발전한 지역마다 그들만의 숫자가 존재했다. 모두가 알고 있는 아라비아 숫자, 어디선가 보거나 들어봤을 법한 바빌론의 쐐기 문자로 된 숫자, 시계에서 많이 볼 수 있는 로마 숫자 외에도 굉장히 많은 숫자들이 존재한다. 현재 우리가 사용하고 있는 10개의 아라비아 숫자로 십진법의 수를 나타낼 수 있다. 바비론의 숫자는 2개뿐인데 60진법의 수를 나타내었다. 동양에서 육십갑자를 사용하는 경우와 비슷한 이유일 것이다.
상위메뉴로 이동
36펜토미노 이야기
-
- 부스번호
- 36
-
- 기관명
- 경남수학문화관 거제수학체험센터
-
- 점심시간
- 12:30~13:30
-
- 부스소개
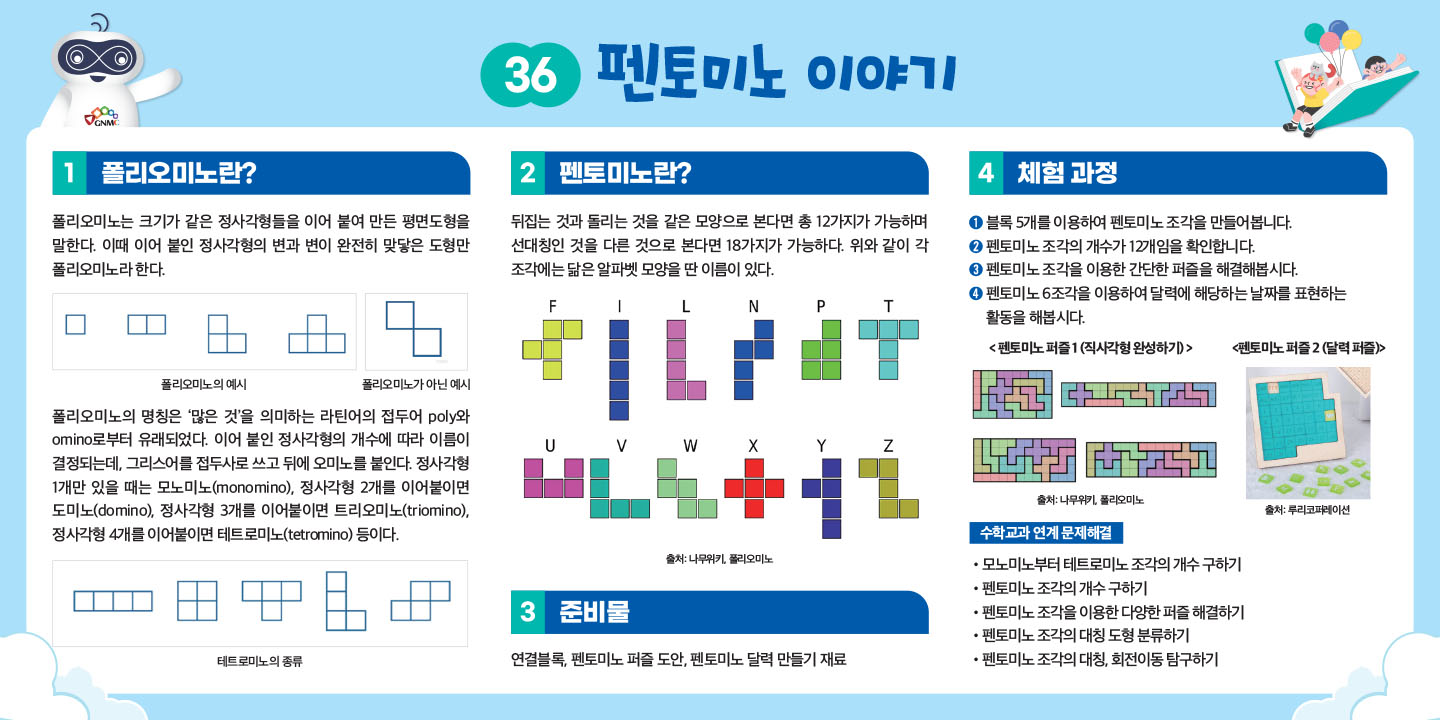
- 폴리오미노는 크기가 같은 정사각형들을 이어 붙여 만든 평면도형을 말한다. 이때 이어 붙인 정사각형의 변과 변이 완전히 맞닿은 도형만 폴리오미노라 한다.
상위메뉴로 이동
37운동으로 즐기는 수학
-
- 부스번호
- 37
-
- 기관명
- 경남수학문화관
-
- 점심시간
- 11:30~12:30
-
- 부스소개
-
상위메뉴로 이동
38놀이로 즐기는 수학
-
- 부스번호
- 38
-
- 기관명
- 경남수학문화관
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 공을 5번 던져서 나온 숫자로 미션을 해결해 봅시다!
상위메뉴로 이동
39산책으로 즐기는 수학 - 양산 워터파크 매쓰투어
-
- 부스번호
- 39
-
- 기관명
- 경남수학문화관
-
- 점심시간
- 11:30~12:30
-
- 부스소개
-
상위메뉴로 이동
40교원 자율 연수
-
- 부스번호
- 40
-
- 기관명
- 경남수학문화관
-
- 점심시간
- 12:30~13:30
-
- 부스소개
-
상위메뉴로 이동
41수학으로 미로탈출
-
- 부스번호
- 41
-
- 업체명
- 주식회사 진교연
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 미로 탈출을 위해 알려진 다양한 방법이 있습니다. 가장 잘 알려진 방법은 수학자 노버트 위너(Norbert Wiener, 1894~1964)가 증명한 벽따르기법(Traversal using right-hand rule, wall follower)입니다. 즉 오른쪽이나 왼쪽 벽을 따라서 손을 떼지 않은 채 걸어 나오는 방법입니다. 우수법 또는 좌수법이라고도 합니다.
상위메뉴로 이동
42가상실험 VlabON 수학으로 이해하는 암호
-
- 부스번호
- 42
-
- 기관명
- 한국과학기술정보연구원
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- VlabON(브이랩온)은 시뮬레이션 소프트웨어를 기반으로 만들어진 온라인 수학·과학 가상실험을 통해 누구나 창의적 연구 능력을 키울 수 있는 학습자 맞춤형 무료 교육 플랫폼입니다. 실제와 유사한 가상 환경에서 자기 주도적인 반복 실험을 통해 세상을 움직이는 수학·과학과 친숙해질 수 있는 공간입니다. 웹 상에서 쉽게 접근하여 학생들이 이론으로만 익힌 원리를 온라인 환경에서 재밌게 실험할 수 있습니다.
상위메뉴로 이동
43다면체 퍼즐장난감 만들기(요시모토 큐브, 칼레이도 사이클)
-
- 부스번호
- 43
-
- 기관명
- 양산교육지원청
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 1971년 일본의 나오키 요시모토가 개발한 다면체퍼즐 장난감이다. 그는 정육면체를 분할하는 방법을 연구하던 중 2개의 별 모양 정방형다면체가 이에 합당하다는 것을 발견했다. 요시모토는 1972년 ‘From cube to space’라는 제목의 개인전에서 자신의 큐브를 소개하고, 나중에 3개의 상용 버전도 개발하였다. 1982년 요시모토 큐브 1번은 박물관 ‘Museum of modern arts’의 영구컬렉션에 포함되었다.
상위메뉴로 이동
444색 정리 지도 가방걸이 만들기
-
- 부스번호
- 44
-
- 기관명
- 양산교육지원청
-
- 점심시간
- 12:30~13:30
-
- 부스소개
- 4색 정리(四色定理)는 평면을 유한 개의 부분으로 나누어 각 부분에 색을 칠할 때, 서로 맞닿은 부분을 다른 색으로 칠한다면 네 가지 색으로 충분하다는 정리이다. 프란시스 거스리 (Francis Guthrie, 1831-1899)는 어느 날 영국의 지도를 색칠하던 중 서로 다른 4가지의 색으로 모두 칠할 수 있다는 것을 발견했다. 이를 들은 그의 동생은 오거스터스 드모르간(Augustus De Morgan, 1806-1871)에게 ‘네 가지 색으로 모든 지도를 칠하는 것’에 관해 질문하게 되고, 이후 이 문제를 ‘4색 문제’라고 부르게 됐다. ‘4색 정리’는 바로 이 ‘4색 문제’를 증명한 것이다.
상위메뉴로 이동
45디지털로 해결하는 A.I 방탈출
-
- 부스번호
- 45
-
- 기관명
- 수학문화도서관
-
- 점심시간
- 11:30~12:30
-
- 부스소개
- 인공지능의 발전 역사 속의 난제들을 게이미피케이션으로 체험을 하며, 주어진 시간 안에 수학융합 문제들을 해결하는 프로그램입니다. 태블릿에 어플을 다운 받아서 진행을 하며, 다채로운 프로그램이 체험객의 상상력과 문제 해결력을 자극 할 것입니다. 방탈출의 짜릿한 즐거움과 수학미션에 도전하는 재미는 물론 추가로 인공지능의 역사도 알아봅시다.
상위메뉴로 이동
46로봇 구슬치기로 연산능력 UP! 문제해결력 UP!
-
- 부스번호
- 46
-
- 기관명
- SW미래채움경남센터
-
- 점심시간
- 12:30~13:30
-
- 부스소개
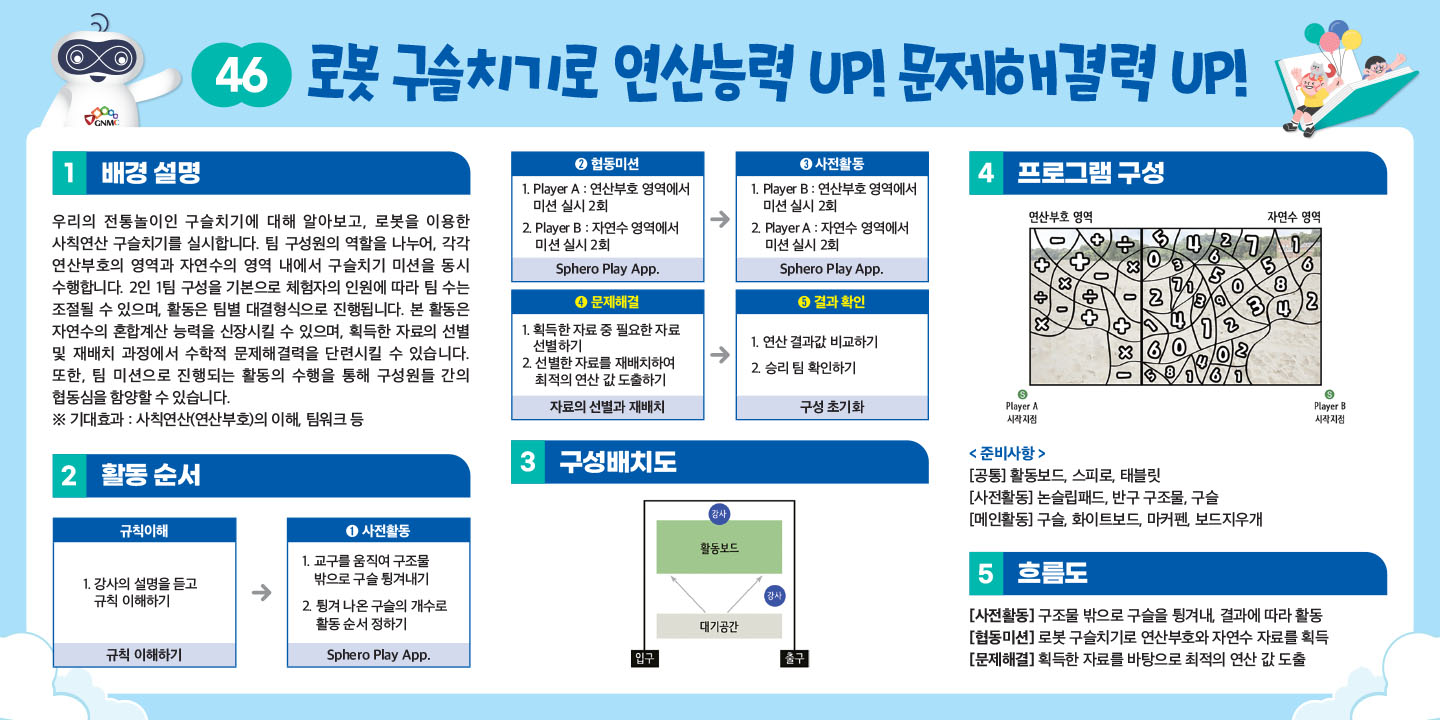
- 우리의 전통놀이인 구슬치기에 대해 알아보고, 로봇을 이용한 사칙연산 구슬치기를 실시합니다. 팀 구성원의 역할을 나누어, 각각 연산부호의 영역과 자연수의 영역 내에서 구슬치기 미션을 동시 수행합니다. 2인 1팀 구성을 기본으로 체험자의 인원에 따라 팀 수는 조절될 수 있으며, 활동은 팀별 대결형식으로 진행됩니다. 본 활동은 자연수의 혼합계산 능력을 신장시킬 수 있으며, 획득한 자료의 선별 및 재배치 과정에서 수학적 문제해결력을 단련시킬 수 있습니다.
상위메뉴로 이동